【Sキャッツ・アイ】設定6の約3000G実戦データから挙動を考察!スランプグラフや各確率はどんな感じ?

チワッスあしのです。
いよいよ登場した6.5号機。有利区間関連の規則が変更になり「ゲーム数上限が4000Gに」そして「同一有利区間での出玉がMYから差枚へ」と変更になりました。いままでは差枚関係なく2400枚出ると終了だったのですが、新規則では有利区間中に吸い込んだ分+2400枚になった、という感じですね。
というわけで今回は、そんな6.5号機第一弾、「Sキャッツ・アイ」の設定6の3000G実戦データを公開します。新規則機の実力やいかに? それではどうぞ。
設定6の3000G実戦データ

まず1000ゲームまでのデータから追っていきましょう。とりあえず補足ですが、本機は出玉ありのリアルボーナスを3種搭載しており、それぞれ「HBB(ハイパービッグボーナス)」「BB(ビッグボーナス)」そして「CB(キャッツボーナス)」と呼びます。以下のデータではそれぞれアルファベットでの略称を使用してます。
AT「キャッツタイム」は開始前に初期ゲーム数上乗せを決める「キャッツチャレンジ」に突入。キャッツチャレンジ中にボーナスを引けば恩恵があるため、キャッツタイムとは分けて記載しています。また総ゲームは「通常ゲーム」と「AT」で分けてますが、「キャッツタイム」はATゲーム数に算入。また仕様上、通常時と高確率状態でリアルボーナスの成立確率が変わりますが、AT終了後の「奪還作戦ステージ」滞在中にどの時点で通常落ちしたのか現状では良くわからないため、とりあえず一律30ゲームで計算しています。要するに30ゲーム以内に引いたボーナスは実際どうあれ「高確率中のボーナス」に算入しとります(このケースは「※」をつけてます)
以上を踏まえてまずは1000ゲームまでのデータがこちら。なお、細かい実戦履歴に関しては最後に3000ゲーム分まとめて記載しています。
前半1000Gの挙動
| ゲーム数 | ||
| 総ゲーム数 | 1117G | |
| 通常ゲーム | 896G | |
| ATゲーム | 221G | |
| 通常時ボーナス | ||
| ボーナス確率 | 1回 | 1/896 |
| HBB | 1回 | 1/896 |
| BB | 0回 | - |
| CB | 0回 | - |
| 高確率状態ボーナス | ||
| ボーナス確率 (※高確率=AT+AT終了後の奪還作戦) |
3回 | 1/85 |
| HBB | 1回 | 1/255 |
| BB | 0回 | - |
| CB | 2回 | 1/127 |
| AT関連 | ||
| AT初当り | 3回 | 1/298 |
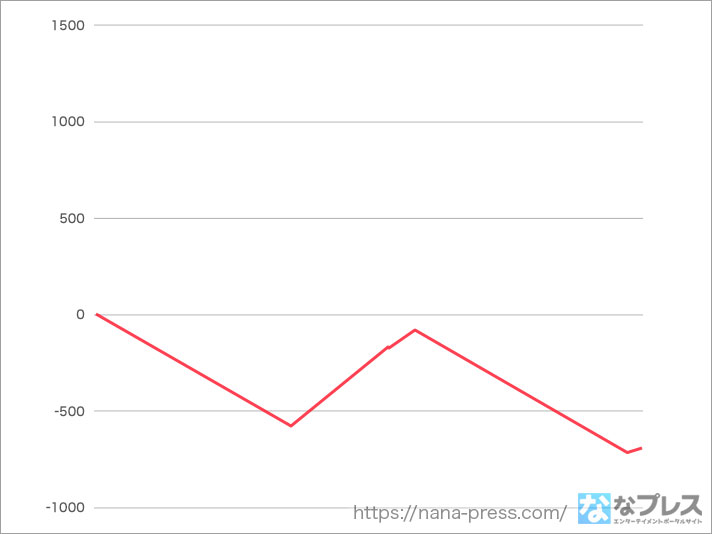
いきなり428Gまで連れていかれるハプニングがありましたがHBB2連発でやや救われ、しかも奪還作戦ステージでのボーナスループに成功します。これ最近のサミー系の機種によく採用されてる「見た目通常のボーナス」が頻繁に成立しており、その消化が終わるまでボーナスの抽選が行われないという仕組みだと思うのですが、必然的にAT終了後は「見た目通常のボーナス」に滞在していないため、結果ボーナス高確率状態となっています。メーカーさんいわく「引き戻し確率は25%オーバー」との事。ただ、「高確率中のボーナス確率」は1/99.9で「全設定共通」であるため、この部分は設定推測の時は分けて考えた方がいいかも。
とにかくこの時点での差枚数はマイナス。1000ゲーム中に400オーバーを2回喰らってるので当たり前っちゃ当たり前ッス。さて次、2000ゲームまでのデータ。ここまで台のポテンシャルを何も引き出せてなかったので割りとドキドキしながら打ってたのですが、やってきましたどでかAT。こちらです。
中盤2000Gまでの実戦データ
| ゲーム数 | ||
| 総ゲーム数 | 732G | |
| 通常ゲーム | 7G | |
| ATゲーム | 725G | |
| 通常時ボーナス | ||
| ボーナス確率 | 0回 | - |
| HBB | 0回 | - |
| BB | 0回 | - |
| CB | 0回 | - |
| 高確率状態ボーナス | ||
| ボーナス確率 (※高確率=AT+AT終了後の奪還作戦) |
10回 | 1/73 |
| HBB | 0回 | - |
| BB | 4回 | 1/182 |
| CB | 6回 | 1/121 |
| AT関連 | ||
| AT初当り | 1回 | 1/7 |
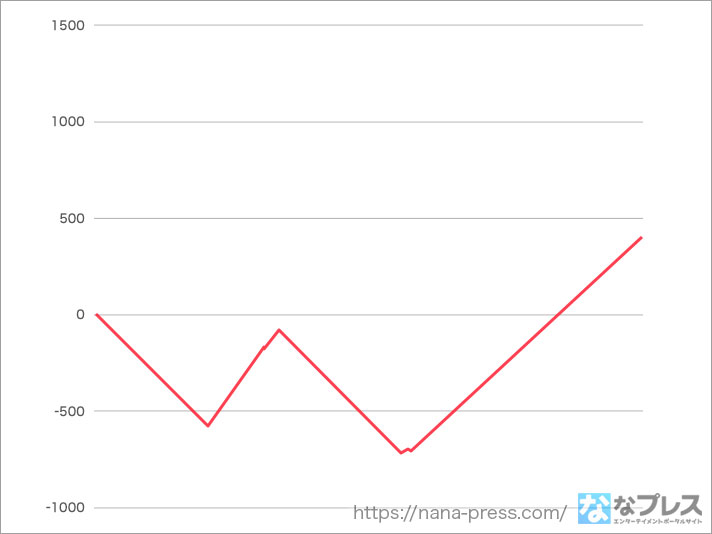
中盤はほぼずっとAT滞在。びっくりしたのがボーナス中の技術介入で+100G級の上乗せが現実的な確率でドンドン出てきたこと。さらに「キャッツチャレンジ」中のボーナス。つまり1G連も出現。今回の恩恵は3桁乗せでしたが、これが普通なのか引き負けてんのかは解析待ちです。

この時点で差枚数的にはプラ転。ただサンプル数的に通常時のボーナス確率が酷い事になっています(笑) はい、最後1000ゲームのデータがこちら。
後半3000Gまでの実戦データ
| ゲーム数 | ||
| 総ゲーム数 | 1014G | |
| 通常ゲーム | 271G | |
| ATゲーム | 743G | |
| 通常時ボーナス | ||
| ボーナス確率 | 2回 | 1/135 |
| HBB | 0回 | - |
| BB | 2回 | 1/135 |
| CB | 0回 | - |
| 高確率状態ボーナス | ||
| ボーナス確率 (※高確率=AT+AT終了後の奪還作戦) |
8回 | 1/103 |
| HBB | 0回 | - |
| BB | 3回 | 1/276 |
| CB | 5回 | 1/166 |
| AT関連 | ||
| AT初当り | 3回 | 1/90 |
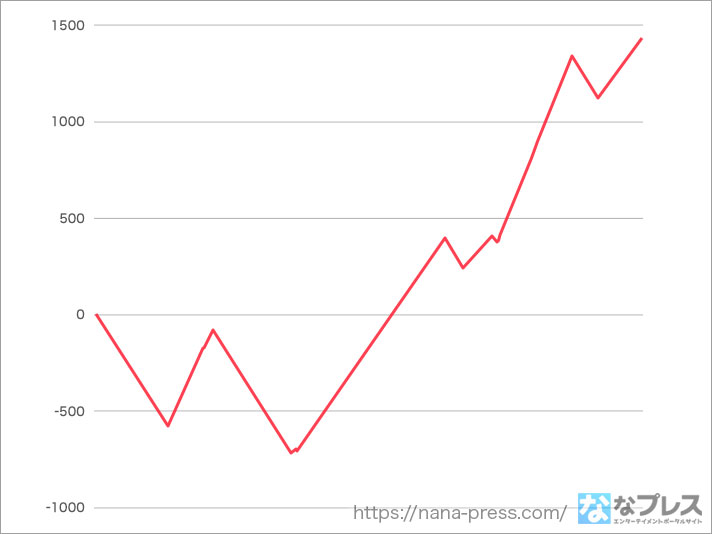
大きなハマりもなく最後まで順調に枚数を増やしていく理想的な展開です。通常時のボーナスも2回あり、これにてギリギリで格好がつく数字になった感じですね。それでは最後に3000Gのトータルのデータを!
最終実戦データ&スランプグラフ
総ゲーム数は2863G。今回はボーナス消化を総ゲーム数に入れてないので、実際にレバーを叩いた回数は3200回くらいになるのかな。とりあえず「約」3000ゲームということでご査収ください。
| ゲーム数 | 当選 | 備考 |
| 278 | 奪還作戦ステージ | 失敗 |
| 428 | HBB | 128枚 +30G |
| (1) | キャッツチャレンジ | 30G |
| (1) | キャッツタイム | |
| (50) | HBB | 128枚 +15G |
| (1) | キャッツチャレンジ | 50G |
| (1) | キャッツタイム | |
| (49) | CB | 66枚 +9G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (46) | END | 410枚 |
| 1 | 奪還作戦ステージ | |
| 4 | ※CB | 71枚 +12G |
| (1) | キャッツチャレンジ | 30G |
| (1) | キャッツタイム | |
| (42) | END | 96枚 |
| 1 | 奪還作戦ステージ | 失敗 |
| 167 | 奪還作戦ステージ | 失敗 |
| 234 | 奪還作戦ステージ | 失敗 |
| 279 | 奪還作戦ステージ | 失敗 |
| 315 | 奪還作戦ステージ | 失敗 |
| 401 | 奪還作戦ステージ | 失敗 |
| 468 | 奪還作戦ステージ | 成功 |
| (1) | キャッツチャレンジ | 30G |
| (1) | キャッツタイム | |
| (30) | END | 0枚 |
| 1 | 奪還作戦ステージ | |
| 7 | ※BB | 92枚 +125G |
| (1) | キャッツチャレンジ | 30G |
| (1) | キャッツタイム | |
| (18) | CB | 105枚 +31G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (44) | CB | 87枚 +7 |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (23) | BB | 104枚 +125G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (169) | CB | 102枚 +4 |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (43) | BB | 107枚 +115G |
| (1) | キャッツチャレンジ | V+100G |
| (1) | CB | 87枚 +24G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (13) | CB | 57枚 +16G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (200) | CB | 81枚 +22G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (133) | BB | 113枚 +56 |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (72) | END | 1105枚 |
| 1 | 奪還作戦ステージ | 失敗 |
| 112 | BB | 77枚 +114G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (71) | CB | 93枚 +7G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (70) | END | 164枚 |
| 1 | 奪還作戦ステージ | 失敗 |
| 28 | ※BB | 107枚 +35G |
| (1) | キャッツチャレンジ | 30G |
| (1) | キャッツタイム | |
| (30) | CB | 78枚 +10G |
| (1) | キャッツチャレンジ | 200G |
| (1) | キャッツタイム | |
| (103) | BB | 110枚 +41G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (70) | CB | 78枚 +36G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (102) | CB | 72枚 +0G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (60) | END | 970枚 |
| 1 | 奪還作戦ステージ | 失敗 |
| 159 | BB | 107枚 +120G |
| (1) | キャッチャレンジ | 10G |
| (1) | キャッツタイム | |
| (59) | BB | 113枚 +43G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (103) | CB | 80枚 +7G |
| (1) | キャッツチャレンジ | 10G |
| (1) | キャッツタイム | |
| (38) | END | 301枚 |
| ゲーム数 | ||
| 総ゲーム数 | 2863G | |
| 通常ゲーム | 1174G | |
| ATゲーム | 1689G | |
| 通常時ボーナス | ||
| ボーナス確率 | 3回 | 1/391 |
| HBB | 1回 | 1/1174 |
| BB | 2回 | 1/587 |
| CB | 0回 | - |
| 高確率状態ボーナス | ||
| ボーナス確率 (※高確率=AT+AT終了後の奪還作戦) |
21回 | 1/86 |
| HBB | 1回 | 1/1816 |
| BB | 7回 | 1/259 |
| CB | 13回 | 1/139 |
| AT関連 | ||
| AT初当り | 7回 | 1/167 |
| 終了画面 | |
| 後ろ姿 | 6回 |
| カフェ | 1回 |
設定6の挙動を考察!
ボーナス確率は判断材料として難しそう。

| 通常時ボーナス | ||
| ボーナス確率 | 3回 | 1/391 |
| HBB | 1回 | 1/1174 |
| BB | 2回 | 1/587 |
| CB | 0回 | - |
| 高確率状態ボーナス | ||
| ボーナス確率 (※高確率=AT+AT終了後の奪還作戦) |
21回 | 1/86 |
| HBB | 1回 | 1/1816 |
| BB | 7回 | 1/259 |
| CB | 13回 | 1/139 |
ではデータを見ながら設定6の挙動を考察してみます。まずボーナス確率なのですが、これ高確率中と通常時でリアボ確率が違うという仕様が結構厄介かも。今回はAT滞在ゲームが非常に長かった影響もあり、通常時のボーナス確率は設定1を大幅に下回る1/391でした。データ表示機から「どっちだったか」を推測するのも困難ゆえ、ボナがめちゃ軽だから6だろう、みたいな判断は危険だと思いました。
CZ成功率やいかに。

| CZ突入率 | ||
| 奪還作戦ステージ成功数 | 7/13 | 53.8% |
| 成功内訳 | ||
| 奪還作戦ステージ内演出成功 | 1回 | |
| 奪還作戦ステージ内のボーナス | 6回 | |
おそらくここにも設定差が振られてると思います。通常時の「奪還作戦ステージ」経由のAT突入率ですが、今回普通に連続演出経由で突入したのは1回でした。あとは「奪還作戦ステージ」中のボーナスから。こっちはポコポコ入ります。ATが長すぎてろくなサンプリングも出来てないんですけども、まあある意味設定6だったらこういう理想的な展開も見えますよくらいに捉えてくださるとありがたし。まだ解析待ちではありますが、公表されてる数字を見る限り、ここに設定差あるはずなんだけどなぁ……。
上乗せゲーム数&キャッツチャレンジの性能差は?

| キャッツチャレンジ | |
| 突入回数 | 25回 |
| 上乗せゲーム数 | |
| 200G | 1回 |
| 100G | 1回 |
| 50G | 1回 |
| 30G | 5回 |
| 10G | 17回 |
「キャッツチャレンジ」では200ゲームが1回、100ゲームが1回、あとはほとんど10ゲームでした。そのゲームで引いた小役(ボーナス含む)でのガチ抽選で、特に出来レース感はなかったです。ただボーナス中のビタ成功時の上乗せはかなり好調で、一撃で100ゲームが複数回ありました。AT中はボーナス確率が「1/99.9」と激軽になるので1回あたりの上乗せは低く抑えてあるのかなと思ったら意外にも豪快。ボナ確率に差がない分、上乗せゲーム数で差をつけてたりしそうな気がしました。あくまで3000ゲーム打った感想に過ぎないので実際どうなのか断言できませんが、その辺も判明ししだい追って「なな徹」にてご案内します!
以上! 少々出来過ぎな感じのデータですが、実際に打つ際の参考にどうぞ! ちなみにビタは他の技術介入機よりちょっと簡単な気がしました。成功率は8割くらい。もっと上手いひとが打つとまた枚数は上乗せされてたかと思います!
 改めてデータみるとホント出来過ぎですなこれ
改めてデータみるとホント出来過ぎですなこれ
INFOMATION
いいね!する
1関連記事
ランキング
-
24時間
-
週間
-
月間
ランキング
-
24時間
-
週間
-
月間
人気機種ランキング
新台導入日
アクセスランキング










































































































この記事にコメントする