【Lストライクウィッチーズ2】設定6の約3000G実戦データを公開！初当たり確率やスランプグラフなど高設定挙動はどんな感じ？
チワッスあしのです！
こちらはサンスリーさんの最新作「Lストライクウィッチーズ2」の実戦データ公開記事です。なんでも純増約7.0枚/GのATを搭載したメリハリのあるスペックということで、どんな感じになってるのか見ていきましょう。なおこちらはまだ内部の具体的な数値などが分からない状態で打っているので、実際にホールで打つ際には「なな徹」にて最新の情報をご確認ください！
設定6の3000G実戦
この機種は通常時にCZ「撃墜チャレンジ」を経由してボーナスを目指すのが基本的な流れになります。撃墜チャレンジはレア役での抽選。今回はCZ突入のデータに契機となった役も併記しています。ちなみにコア図柄は出現数のみ記載。「コア1」「コア2」など。出現リールにより期待値に変化がある可能性もありますが、それあとから気づいたんでメモってません（すまん）
それではみていきましょう。どうぞ。
前半戦1000Gまで
| G数 | 当選 | 備考 |
| 219 | 撃墜チャレンジ | 契機:チャンス目orコア1 |
| 363 | 撃墜チャレンジ | 契機:強チェリー |
| 614 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-18型 +40G |
|
| 56 | ごほうびAT | 200枚 |
| ネウロイバトル | X-12型 +30G |
|
| 42 | 終了 | 513枚 |
| ゲーム数 | ||
| 種類 | G数 | |
| 総ゲーム数 | 757G | |
| 通常ゲーム数 | 584G | |
| CZゲーム数 | 30G | |
| ボーナスゲーム数 | 15G | |
| ネウロイバトルゲーム数 | 98G | |
| ATゲーム数 | 30G | |
| 通常時 | ||
| 種類 | 回数 | 出現率 |
| CZ「撃墜チャレンジ」突入回数 | 2回 | 1/307.0 |
| ネウロイバトル成功/突入 | 1/2(50％) | |
| AT初当たり | ||
| 種類 | 回数 | 出現率 |
| AT「ごほうびAT」突入回数 | 1回 | 1/614.0 |
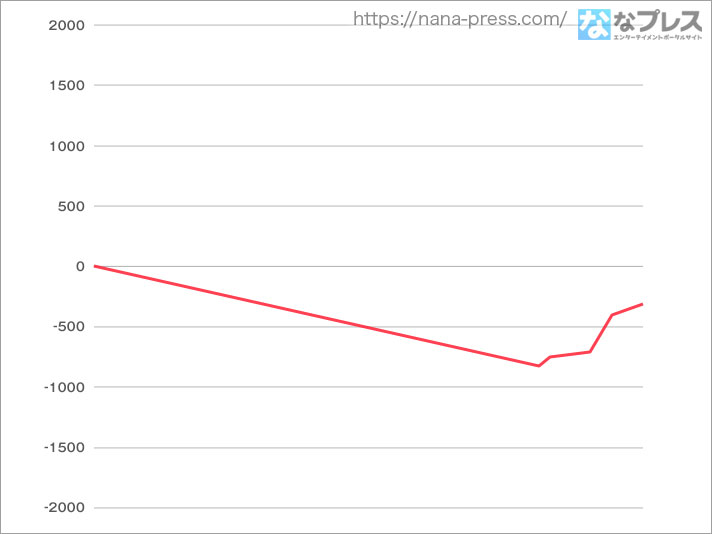
フローがシンプルなのでデータもスッキリ。というかいきなり600Gくらいハマった上に謎当たりからスタートです。先に言っとくと今回600G前後で謎当たりが複数回発生。もしかしてこれモード天井なのかな……？
記念すべき最初のATのバトルは「ネウロイ18型」でした。これ型によって期待度（というか保証ゲーム数）が違うらしく、18型は期待度中のやつ。あ、結構出るんだな18型、とか思ったのですが、これ以降は1回も出ず。全部期待度が小の「12型」でした。ぐぬぬ。ともあれ初回のATはなんとか1勝をもぎ取り500枚くらいで終了。いやこれあんまり伸びなくてもとりあえず500枚くらい取れるのはデカいですな。イメージとしては中ハマりくらいして中くらい出る、というのを繰り返す感じかもしれません。
さあ次中盤戦です。
中盤戦2000Gまで！
| G数 | 当選 | 備考 |
| 226 | 撃墜チャレンジ | 契機:チャンス目orコア1 |
| 675 | 撃墜チャレンジ | 契機:コア1 |
| 815 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-12型 +30G |
|
| 55 | ごほうびAT | 300枚 |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 478枚 |
| ゲーム数 | ||
| 種類 | G数 | |
| 総ゲーム数 | 973G | |
| 通常ゲーム数 | 785G | |
| CZゲーム数 | 30G | |
| ボーナスゲーム数 | 15G | |
| ネウロイバトルゲーム数 | 100G | |
| ATゲーム数 | 43G | |
| 通常時 | ||
| 種類 | 回数 | 出現率 |
| CZ「撃墜チャレンジ」突入回数 | 2回 | 1/407.5 |
| ネウロイバトル成功/突入 | 1/2(50％) | |
| AT初当たり | ||
| 種類 | 回数 | 出現率 |
| AT「ごほうびAT」突入回数 | 1回 | 1/815.0 |
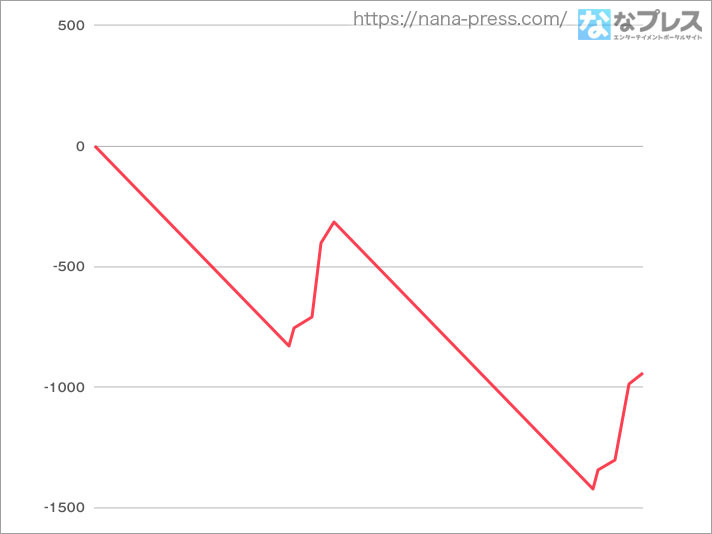
ぐは、800Gハマり。そしてまた謎当たり。これは参考になるのか果たして……！ というか今気づいたんですけどこれコアを狙えで目押しミスってる可能性あるのかな。だからほんとはコア1とかで当たってたり？ いやぁさすがに25年くらいパチスロ打っててそれはないと思うんだけども、もしそうだったらほんますんません。600Gとか800Gとかの謎当たりの正体については、多分そのうち「なな徹」でも明らかにされるでしょう。マジでゲーム数当選がなんもない場合は俺の目押しミスです。
ともあれ2回目のATも1勝で終了。かなりキツイ状況ですが最後に見せ場は訪れるのか！ ラストどうぞ！
ラスト！3000Gまで！
| G数 | 当選 | 備考 |
| 239 | 撃墜チャレンジ | 契機:コア1 超高確 |
| 525 | 撃墜チャレンジ | 契機:強チェリー |
| 615 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-12型 +30G |
|
| 27 | ごほうびAT | 300枚 |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 508枚 終了:キャラ4人 |
| 136 | 撃墜チャレンジ | 契機:強チェリー |
| 143 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 126枚 |
| 38 | 撃墜チャレンジ | 契機:チャンス目 |
| 54 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G ダメージ引き継ぎ発生 |
|
| 31 | ごほうびAT | 500枚 |
| ネウロイバトル | X-12型 +30G |
|
| 33 | ごほうびAT | 200枚 |
| ネウロイバトル | X-12型 +30G |
|
| 44 | 終了 | 736枚 |
| 90 | 撃墜チャレンジ | 契機:コア2 |
| 108 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G |
|
| 38 | ごほうびAT | 400枚 |
| ネウロイバトル | X-12型 +30G |
|
| 37 | 終了 | 562枚 |
| ヤメ | ||
| ゲーム数 | ||
| 種類 | G数 | |
| 総ゲーム数 | 1480G | |
| 通常ゲーム数 | 849G | |
| CZゲーム数 | 71G | |
| ボーナスゲーム数 | 60G | |
| ネウロイバトルゲーム数 | 300G | |
| ATゲーム数 | 200G | |
| 通常時 | ||
| 種類 | 回数 | 出現率 |
| CZ「撃墜チャレンジ」突入回数 | 5回 | 1/184.0 |
| ネウロイバトル成功/突入 | 4/8(50％) | |
| AT初当たり | ||
| 種類 | 回数 | 出現率 |
| AT「ごほうびAT」突入回数 | 4回 | 1/230.0 |
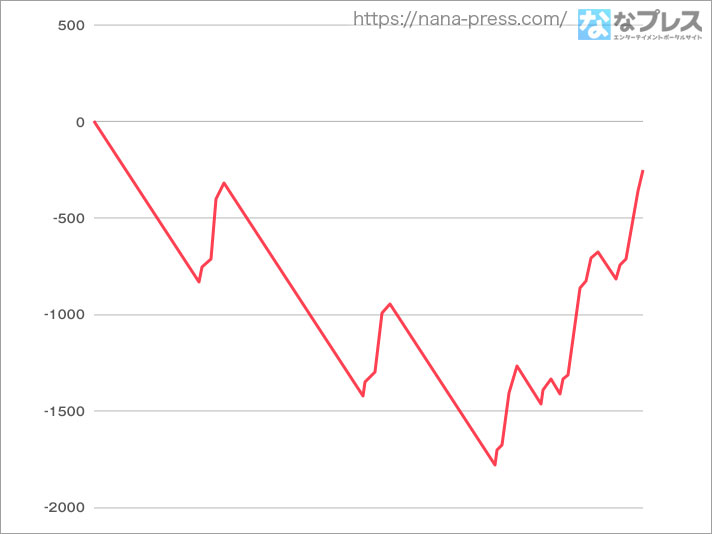
うお、最後はちょっと頑張った！ 出だしこそいきなり600Gまでハマって死にかけてますがそこから先はやっと「撃墜チャレンジ」が仕事し始めてテンポよく当たり、ダメージ引き継ぎも発生してまとまったメダルをポンポンとゲットした感じ。これで一気に負債を減らしてほぼトントンくらいまで持っていくことに成功です。これ2戦勝利が1回発生したんですけども、あと1回で上位チャレンジだった、と考えるとそれなりにアツかったッスな。まあ残り1勝が遠いのかもしれませんが……。
さて、それでは全体のグラフをみてみましょうかね！
最終データ＆グラフ！
| G数 | 当選 | 備考 |
| 219 | 撃墜チャレンジ | 契機:チャンス目orコア1 |
| 363 | 撃墜チャレンジ | 契機:強チェリー |
| 614 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-18型 +40G |
|
| 56 | ごほうびAT | 200枚 |
| ネウロイバトル | X-12型 +30G |
|
| 42 | 終了 | 513枚 |
| 226 | 撃墜チャレンジ | 契機:チャンス目orコア1 |
| 675 | 撃墜チャレンジ | 契機:コア1 |
| 815 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-12型 +30G |
|
| 55 | ごほうびAT | 300枚 |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 478枚 |
| 239 | 撃墜チャレンジ | 契機:コア1 超高確 |
| 525 | 撃墜チャレンジ | 契機:強チェリー |
| 615 | ストライクボーナス | 契機:ゲーム数 |
| ネウロイバトル | X-12型 +30G |
|
| 27 | ごほうびAT | 300枚 |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 508枚 終了:キャラ4人 |
| 136 | 撃墜チャレンジ | 契機:強チェリー |
| 143 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G |
|
| 45 | 終了 | 126枚 |
| 38 | 撃墜チャレンジ | 契機:チャンス目 |
| 54 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G ダメージ引き継ぎ発生 |
|
| 31 | ごほうびAT | 500枚 |
| ネウロイバトル | X-12型 +30G |
|
| 33 | ごほうびAT | 200枚 |
| ネウロイバトル | X-12型 +30G |
|
| 44 | 終了 | 736枚 |
| 90 | 撃墜チャレンジ | 契機:コア2 |
| 108 | ストライクボーナス | 契機:撃墜チャレンジ |
| ネウロイバトル | X-12型 +30G |
|
| 38 | ごほうびAT | 400枚 |
| ネウロイバトル | X-12型 +30G |
|
| 37 | 終了 | 562枚 |
| ヤメ | ||
| ゲーム数 | ||
| 種類 | G数 | |
| 総ゲーム数 | 3210G | |
| 通常ゲーム数 | 2218G | |
| CZゲーム数 | 131G | |
| ボーナスゲーム数 | 90G | |
| ネウロイバトルゲーム数 | 498G | |
| ATゲーム数 | 273G | |
| 通常時 | ||
| 種類 | 回数 | 出現率 |
| CZ「撃墜チャレンジ」突入回数 | 9回 | 1/261.0 |
| ネウロイバトル成功/突入 | 6/12(50％) | |
| AT初当たり | ||
| 種類 | 回数 | 出現率 |
| AT「ごほうびAT」突入回数 | 6回 | 1/391.5 |
後半は優秀なんですけど、はじめの2000Gが不味い。逆に言うとこんなボロボロの状態からよくここまで持ち直しました。最初ボロクソだった理由はかなりハッキリしてまして、要は「撃墜チャレンジ」でやれてなさすぎるんですね。これがちゃんと出来てたら全然プラスでした。実は「撃墜チャレンジ」経由の当たりは最後に3回まとめてきてるだけで、ほかは全部ゲーム数（だと思う）当たりなんですね。これはスペック上の説明とはぜんぜん違う挙動であり、俺1人だけ別ゲーを打ってる感じであります。撃墜チャレンジそのものの突入率はそんなに悪くないと思うので、ちゃんと突破できてればもうちょい違った結果になってたと思います。
では今回のデータから高設定の挙動を推測してみましょう。
高設定の挙動を推測！
初当たり確率からみてみる！
| 今回の初当たり確率 | ||
| 種類 | 回数 | 確率 |
| CZ「撃墜チャレンジ」 | 9回 | 1/261.0 |
| ストライクボーナス | 6回 | 1/391.5 |
| CZ確率・ボーナス初当たり確率 | ||
| 設定 | CZ 「撃墜チャレンジ」 |
ストライクボーナス |
| 1 | 1/245.6 | 1/432.5 |
| 2 | 1/245.0 | 1/420.7 |
| 3 | 1/244.8 | 1/409.6 |
| 4 | 1/243.2 | 1/389.1 |
| 5 | 1/242.6 | 1/370.0 |
| 6 | 1/240.6 | 1/349.3 |
※なな徹調べ
初当たり確率はこんな感じ。スペックでいうとだいたい中間設定くらいに落ち着いてますが、これ後半に2桁連を2発ブチかましてやっとそれなので。多分それなかったら設定8くらいでした。「撃墜チャレンジ」の確率はこれを書いてる時点でまだ出てませんがそんなに悪くなさげな気がしてます。全部で9回あたり。突破したのが3回。しかもその3回は固まっていて、要は6連続で外してます。考えうるなかでだいぶアカンやつですが、それでもこの数値に収まってるというのは撃墜チャレンジ自体がやっぱちゃんと引けてたからなんですな。ちょっとまだ詳細は出てませんが、多分「撃墜チャレンジ」自体にも設定差があると思われますし、ここはしっかりチェックしながら打ったほうが良いところかもしれません。実際ほんとにそうなのかは、「なな徹」での情報公開を待ちましょう。
撃墜チャレンジの当選契機！
| 今回のCZ「撃墜チャレンジ」当選契機 | |
| 種類 | 回数 |
| コア図柄1個停止 | 2回 |
| コア図柄2個停止 | 1回 |
| チャンス目 orコア図柄1個停止 |
2回 |
| チャンス目 | 1回 |
| 強チェリー | 3回 |
はいこれ結構重要な気がします。「コア1」がめちゃ仕事してるんですね。ちょっと状況が混み入っててコア1だったと断言できねぇのが2個ありますが、それにしたって高頻度のコア1からの当選がこんだけあるのはいかにも高設定くさい挙動だと思います。これで設定差が無かったらヤバいんですけども、俺はここは「設定差アリ」と予想。これもまだ正確には分からない情報なので、「なな徹」にて答え合わせをお願いいたします！
はい、以上がサンスリーさんの最新機種「Lストライクウィッチーズ2」のデータ公開記事でした！
パンツじゃないから恥ずかしくないもん！（これしか知らない）
INFOMATION
バックナンバーはこちら
「浅草に住むサブカル・ギャンブル系フリーライター。ペンネームの由来は4号機『バクチョウ（メーシー）』の主人公あしの君から。いろんな所でちょいちょい書かせて頂いております。
いいね！する
0関連記事
ランキング
-
24時間
-
週間
-
月間
ランキング
-
24時間
-
週間
-
月間
人気機種ランキング
新台導入日
2025年11月17日
2025年12月01日
2025年12月08日
2025年12月22日
2026年01月05日
2026年01月19日
2026年02月02日
2025年11月04日
2025年10月20日
2025年10月06日
2025年09月22日
2025年09月08日
アクセスランキング
この記事にコメントする